Assignment 9
Pedal Triangles
Nicolina Scarpelli
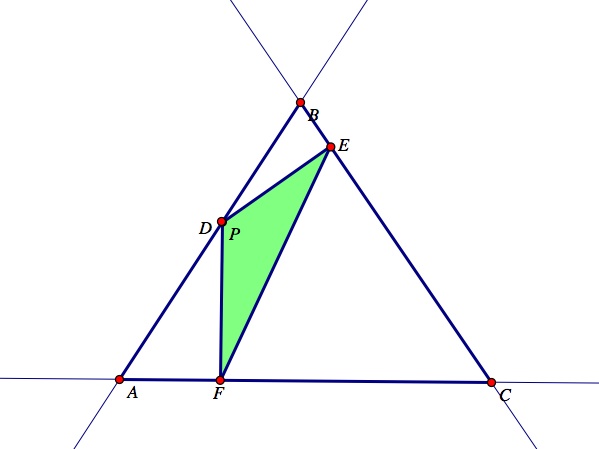
In this assignment, we are going to utilize the program Geometer's Sketchpad to explore various constructions of pedal triangles. Let triangle ABC be any triangle. Then, given a point P in the plane, the pedal triangle for the pedal point P is the triangle whose polygon vertices are the feet of the perpendiculars from P to the sides of the triangle ABC.
Investigation 1:
Steps for constructing a pedal triangle using Geometer's Sketchpad:
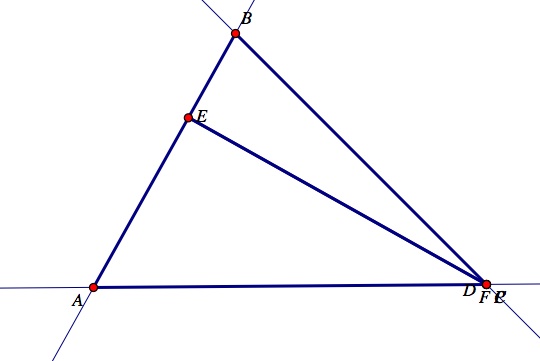
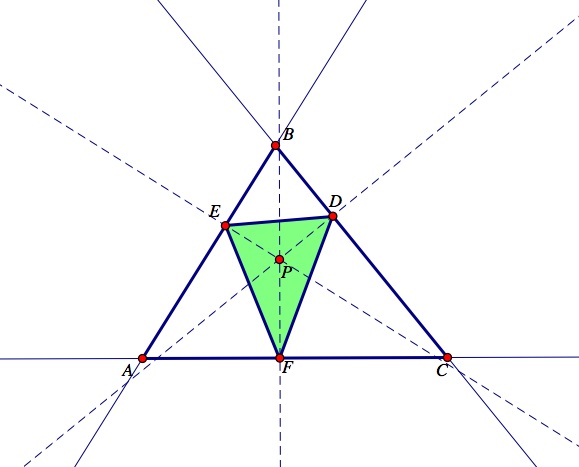
(1) Construct a triangle ABC by plotting three non-colinear points A, B, and C. Then, construct lines between the points to make a triangle. Next, plot an arbitrary point, P, anywhere in plane.
(2) Now, construct perpendicular lines from the pedal point, P, to the sides of the triangle ABC.
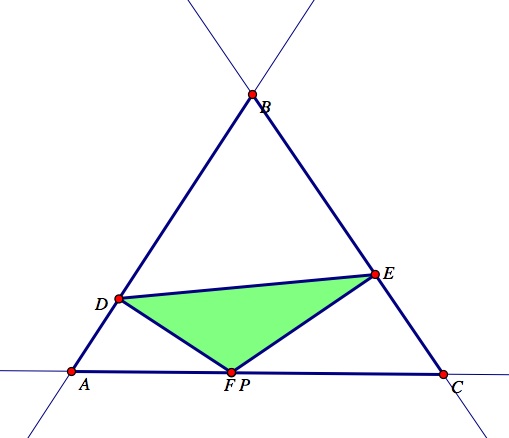
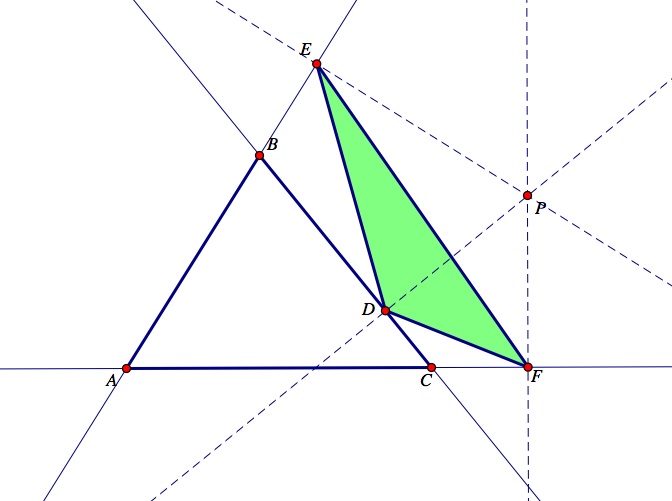
(3) Next, construct the intersections of the perpendicular lines and the sides of the triangle. Label these intersections D, E, and F. Now, construct the line segments that connect the three intersections of the triangle to form a new triangle DEF. Observe the picture below where ABC is the original triangle, and the pedal point P is located outside of the triangle ABC. The pedal triangle DEF created is shown in green.
Pedal point, P, located outside of the triangle ABC.
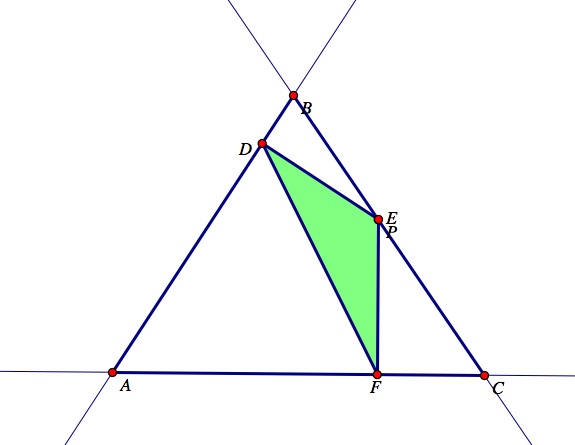
Pedal point, P, located inside of the triangle ABC.
Click here for a GSP script tool for the construction of a Pedal Triangle. Observe that there is no restriction on where the pedal point P can be located in the plane; it can be inside or outside the triangle ABC. Translate the pedal point P using the script tool to observe the relationship between the pedal point P, the pedal triangle DEF, and the original triangle ABC.
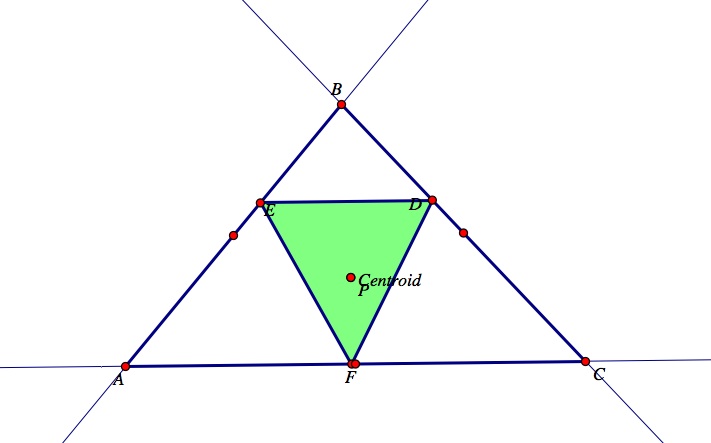
Investigation 2: Let's observe what happens when the pedal point P is varied. First we will see what happens when the pedal point, P, is located at the centroid of the triangle ABC.
Steps to construct the centroid of a triangle ABC:
(1) First, begin by constructing triangle ABC by plotting three points A,B, and C and connecting them with segments. Then, construct the midpoints of these three segments.
(2) Now, construct the three medians of a triangle, which are the segments from a vertex of triangle ABC to the midpoint of the opposite side. The point of concurrency of the three medians is the centroid.
Click here for a GSP construction and click the animation button labeled "Move P - Centroid" to observe the movement of the pedal point, P, to the centroid of the triangle ABC. Notice, when the pedal point P is moved to the centroid, the pedal triangle now has all three vertices on the sides of the original triangle ABC. Recall from assignment 4, that regardless of the size or shape of triangle ABC, the centroid will always lie inside of triangle ABC. Since this means the pedal point, P, will always lie inside triangle ABC as well, the vertices of the pedal triangle DEF will remain along the sides of triangle ABC.
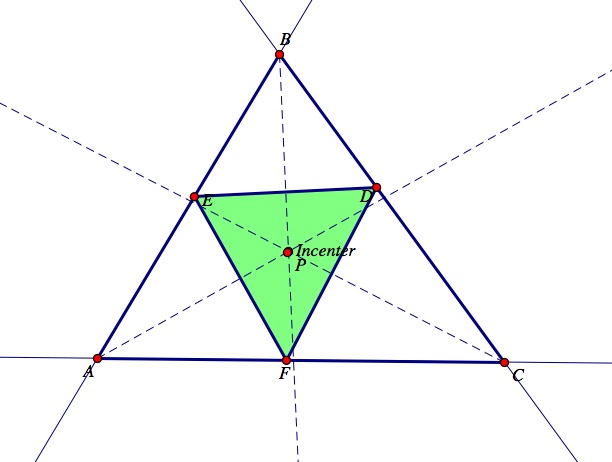
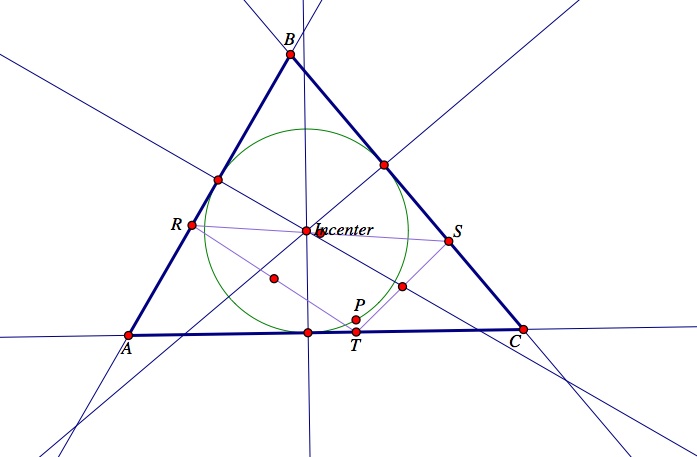
Next, let's explore what will happen to the pedal triangle DEF if the pedal point, P, is the incenter of triangle ABC?
Steps to construct the incenter of a triangle ABC:
(1) Construct a triangle ABC just like above. Now, construct the three angle bisectors of the angles of the triangle. Do this by clicking the two sides surrounding the angle that you want a bisector through, and then go to to construct "angle bisector".
(2) Construct the point of concurrency of the three angle bisectors. This is the incenter of the circle.
Click here for a GSP construction and click the animation button labeled "Move P - Incenter" to observe the movement of the pedal point, P, to the incenter of the triangle ABC. Notice, when the pedal point, P, is the incenter of triangle ABC, the pedal triangle DEF has all three vertices on the sides of triangle ABC. Recall from assignment 4, that regardless of the size or shape of triangle ABC, the incenter will always be located inside of the triangle ABC just like the centroid. Use the GSP construction to vary the sides of triangle ABC, and observe that when the pedal point,P, is the incenter, the vertices of the pedal triangle DEF will always remain on the sides of triangle ABC.
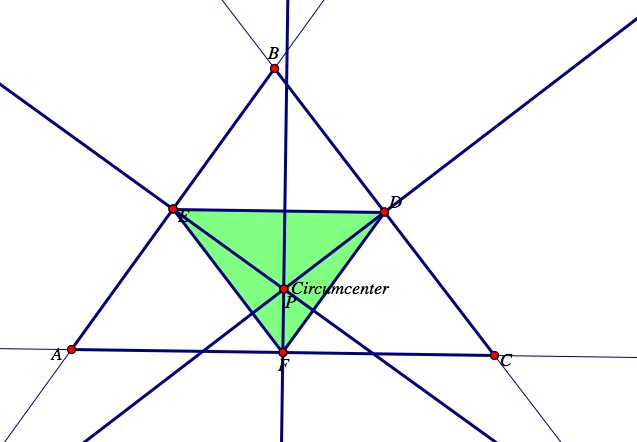
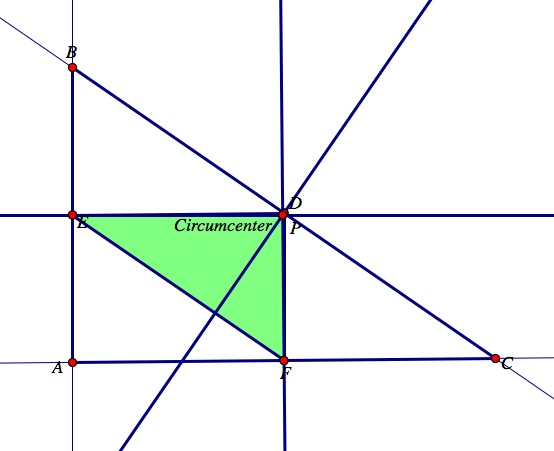
Now, let's observe what will happen to the pedal triangle DEF if the pedal point, P, is the circumcenter of triangle ABC? What if the circumcenter is located outside of triangle ABC?
Steps to construct the circumcenter of triangle ABC:
(1) Construct a triangle ABC by plotting points A, B, and C and constructing line segments between the points. Then, construct midpoints of each of the segments.
(2) Construct perpendicular bisectors of the triangle, which are the lines perpendicular to the sides of a triangle through the midpoints of the side. The point of concurrency of three of these perpendicular bisectors is the circumcenter of triangle ABC.
Click here for the GSP construction and click the animation button labeled "Move P - Circumcenter" to observe the movement of the pedal point, P, to the circumcenter of the triangle ABC.
Notice the pedal triangle DEF has all three vertices on the sides of triangle ABC just like before. However, each of the vertices also lie along the perpendicular bisectors of triangle ABC. Use the GSP construction to change the vertices of ABC to observe what happens to the pedal triangle DEF when the original triangle ABC is obtuse, acute, and a right triangle. Notice that no matter what shape triangle ABC is, when the pedal point, P, is moved to the circumcenter, the vertices of the pedal triangle DEF will remain on the perpendicular bisectors and the sides of triangle ABC. Therefore, when the pedal point P is the circumcenter of triangle ABC, the pedal triangle DEF will always be inside triangle ABC even though the circumcenter can be located outside of triangle ABC.
When triangle ABC is acute, its circumcenter is located inside the triangle ABC. Notice, when the pedal point, P, is moved to the circumcenter, the vertices D, E, and F of the pedal triangle DEF lie on both the sides of triangle ABC and on the perpendicular bisectors. Observe the image below.
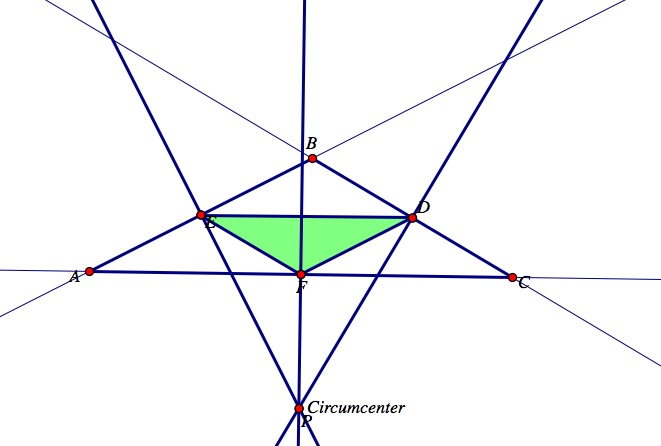
When triangle ABC is obtuse, its circumcenter is located outside of the triangle. However, the vertices of the pedal triangle DEF still lie on the perpendicular bisectors and on the sides of triangle ABC. Observe the image below.
When triangle ABC is a right triangle, its circumcenter is located inside triangle ABC. When the pedal point, P, is moved to the circumcenter, the pedal triangle DEF is located inside triangle ABC and the vertices of DEF are located on the sides. In addition, the vertices of DEF still lie on the perpendicular bisectors. Observe the image below.
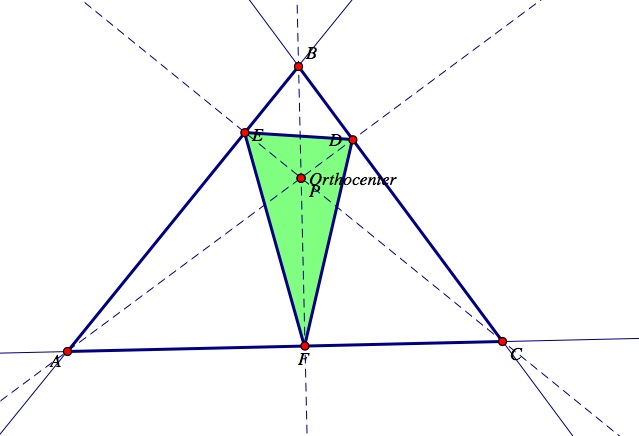
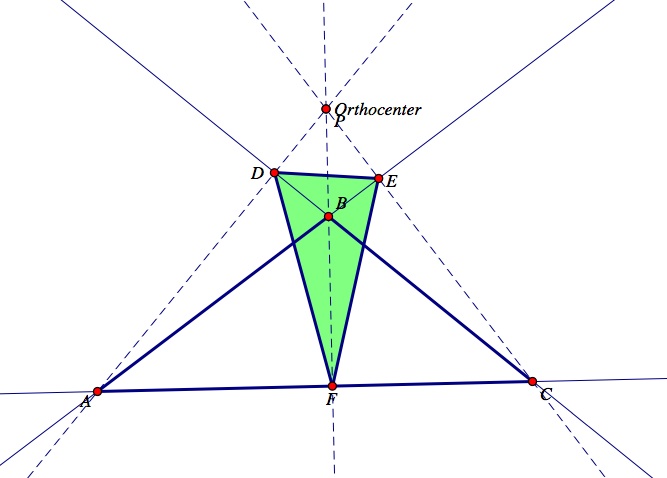
Now, let's observe what will happen to the pedal triangle DEF if the pedal point, P, is the orthocenter of triangle ABC? What if the orthocenter is located outside of triangle ABC?
Steps to construct the orthocenter of triangle ABC:
(1) First, construct a triangle ABC as done for the previous exercises. Next, construct the three altitudes of triangle ABC. The altitudes of triangle ABC are the perpendicular segments from the vertex to the opposite side of the triangle.
(2) The point of concurrency of the three altitudes is the orthocenter of triangle ABC.
Click here for the GSP construction and click the animation button labeled "Move P - Orthocenter" to observe the movement of the pedal point, P, to the orthocenter of the triangle ABC.
Observe where the pedal triangle DEF and its vertices are located when the orthocenter is located inside triangle ABC (i.e. when triangle ABC is acute).When triangle ABC is acute, the vertices D, E, and F of the pedal triangle lie on the sides of triangle ABC and on the altitudes.
Observe where the pedal triangle DEF and its vertices are located when the orthocenter is located outside triangle ABC (i.e. when triangle ABC is obtuse). Observe the image below to see when triangle ABC is obtuse, its orthocenter is located outside of it. Notice the vertices of the pedal triangle DEF lie on the altitudes; however, they are not on the sides of triangle ABC.
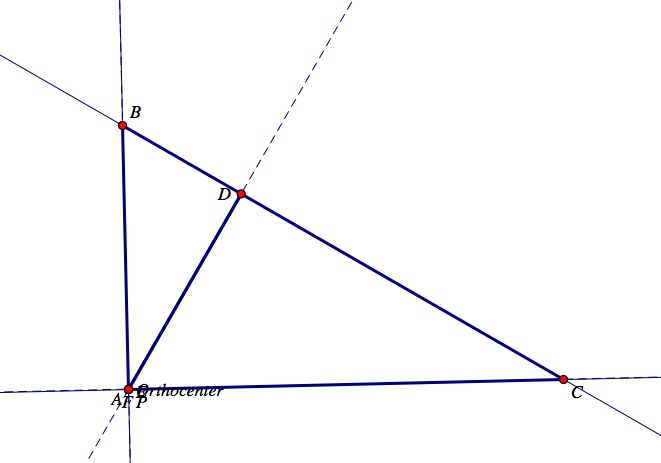
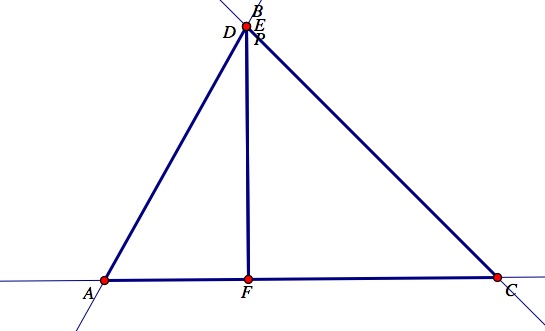
Observe where the pedal triangle DEF and its vertices are located when the orthocenter is a vertice of triangle ABC below (i.e. when triangle ABC is a right triangle).
What is the difference between the movement of the pedal point, P, to the orthocenter compared to the circumcenter? Notice that when the pedal point, P, is the orthocenter each of the vertices D, E, F of the pedal triangle lie along the altitudes of triangle ABC. Use the GSP construction above to move the vertices of triangle ABC. You can see that no matter what type of triangle ABC may be, when the pedal point, P, is moved to the orthocenter of ABC, the vertices of the pedal triangle DEF will remain on the altitudes of triangle ABC every time. Notice that when triangle ABC is a right triangle and the pedal point P is the orthocenter of triangle ABC, the pedal triangle DEF degenerates into a line segment. We will focus more on this concept of the pedal triangle degenerating into a line segment further into the investigations.
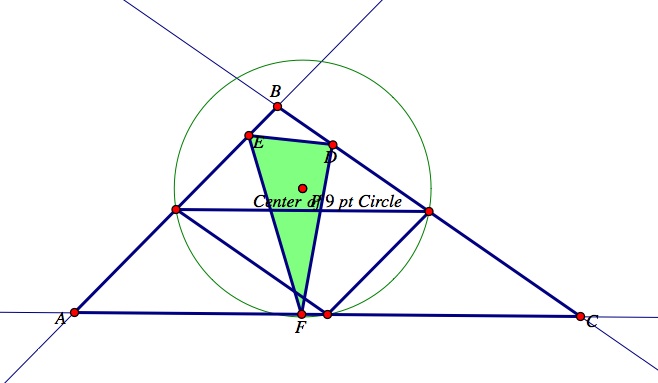
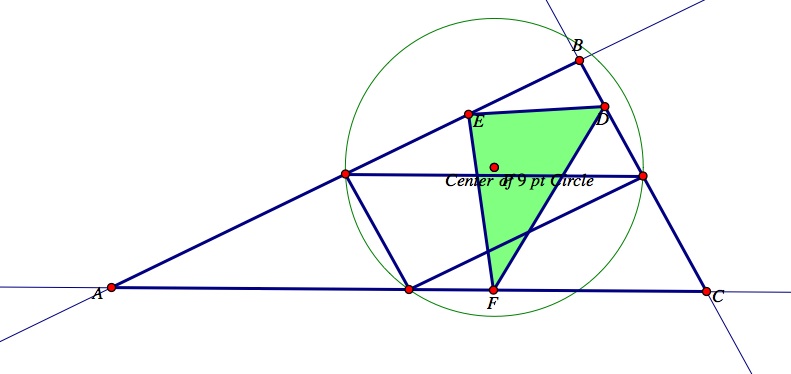
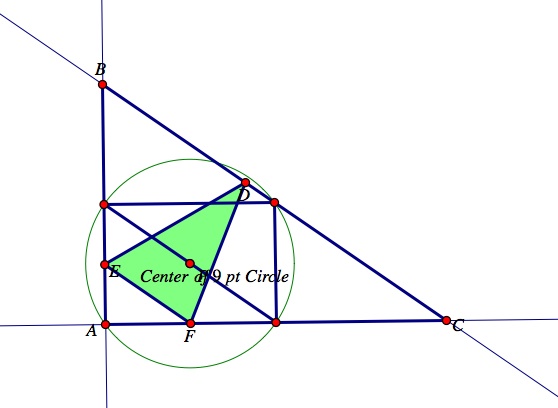
Now, let's observe what happens if the pedal point P is the Center of the nine point circle for triangle ABC?
Steps to construct the center of a nine point circle for triangle ABC:
(1) Construct a triangle ABC just like above. Now, construct the medial triangle inside triangle ABC. In order to construct the medial triangle, you must construct the midpoints of the three segments of triangle ABC. Then, construct the three segments that join the midpoints. This is the medial triangle of triangle ABC.
(2) Next, construct the circumcenter of the medial triangle. To do this, construct the midpoints of the segments of the medial triangle you just created. Construct perpendicular bisectors of the triangle, which are the lines perpendicular to the sides of a triangle through the midpoints of the side. The point of concurrency of the three perpendicular bisectors is the circumcenter. The circumcenter of the medial triangle is in fact the center of the 9 point circle.
Click here for the GSP construction and press the animate button "Move P - Center of 9 pt Circle" to observe the movement of the pedal point, P, to the center of a 9 point circle. Move the vertices of triangle ABC to explore different types of triangles, and observe what happens to the pedal triangle DEF when the pedal point is the center of a 9 point circle. The vertices D, E, and F of the pedal triangle DEF appear to lie on the sides of triangle ABC even when the vertices A, B, and C are shifted.
When ABC is an acute triangle
When triangle ABC is an obtuse triangle.
When triangle ABC is a right triangle.
A question to think about: Will the vertices of the pedal triangle DEF ever lie exactly on the 9 point circle? Use the GSP construction provided to continue this exploration!
Now, let's observe what happens if the pedal point, P, is located on a side of the triangle ABC? Click here for the GSP construction, and move the pedal point, P, to any side of triangle ABC to observe the changes made to the pedal triangle DEF.
Pedal point, P, is located on the side AB of triangle ABC. Notice that the pedal point, P, becomes the vertice D of the pedal triangle DEF.
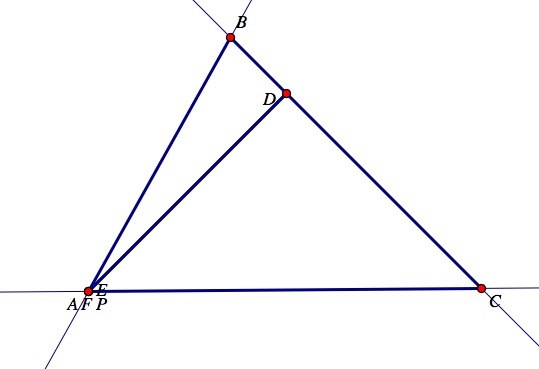
Pedal point, P, is located on the side AC of triangle ABC. Notice that the pedal point, P, becomes the vertice F of the pedal triangle DEF.
Pedal point, P, is located on side BC of triangle ABC. Notice that the pedal point, P, becomes the vertice E of the pedal triangle DEF.
Observe from the pictures above and the GSP construction when the pedal point, P, moves to one of the sides of triangle ABC, we can see that P becomes one of the vertices of the pedal triangle DEF. What happens to the pedal triangle when triangle ABC is acute? What happens to the pedal triangle when triangle ABC is obtuse? Where are the vertices of the pedal triangle DEF located? By moving point P to different points on each side of our triangle ABC, we can see that point P will always be the same point as one of the vertices of the pedal triangle DEF.
Last but not least, let's observe what will happen if the pedal point, P, is one of the vertices of triangle ABC?
Click here for the GSP construction and click the animate buttons "Move P to B", "Move P to A", and "Move P to C" to observe what happens to the pedal triangle DEF when the pedal point, P, is moved to the vertices of triangle ABC.
When the pedal point, P, moves to one vertex of triangle ABC, we can see all three vertices of the pedal triangle DEF are collinear. By viewing the animation, we can see each time point P is moved to a vertex of triangle ABC, the vertices of the pedal triangle DEF will be collinear. By moving point P to different vertices of our triangle ABC, we can see that point P and all three vertices of the pedal triangle DEF are collinear. Observe the images below.
Moving the Pedal Point P to vertex A.
Moving the Pedal Point P to vertex B
Moving the Pedal Point P to vertex C
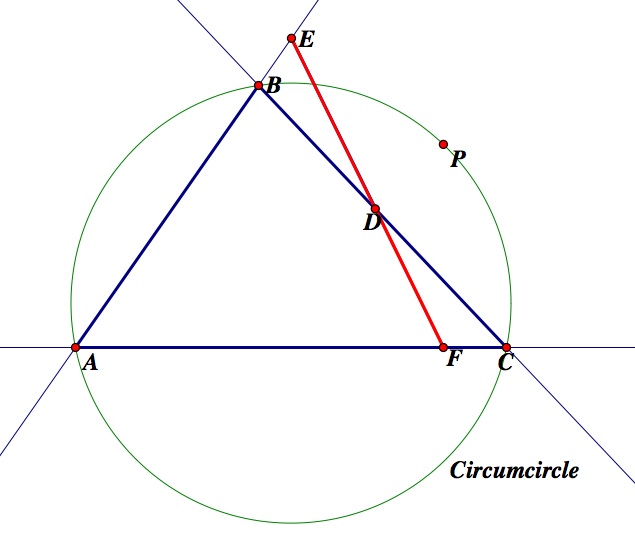
Notice, when the three vertices of the pedal triangle DEF are collinear, the pedal triangle is called a degenerate triangle because it degenerates into a line. To continue what we pointed out above, as you can see, the pedal triangle DEF no longer looks like a triangle; however, it appears to be a line segment. This line segment is known as the Simson Line. This also happens when the pedal point, P, is located on the circumcircle of triangle ABC. Observe the picture below. Click here for a GSP construction of the circumcircle of triangle ABC. Animate the pedal point P to observe the movement of the pedal point, P, around the circumcircle and the Simson line created (shown in red).
Want to explore more with the Simson Line? Create different explorations and try to find all conditions in which the three vertices of the Pedal Triangle DEF are colinear!
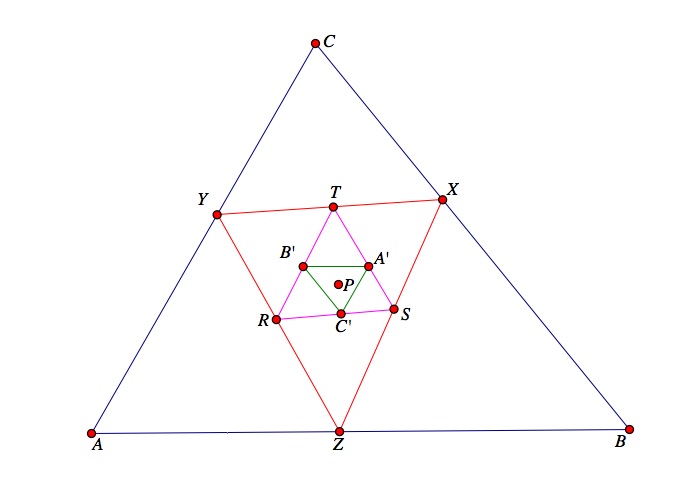
Investigation 3: Prove the pedal triangle of the pedal triangle of the pedal triangle of a point is similar to the original triangle. That is, show that the pedal triangle A'B'C' of pedal triangle RST of the pedal triangle XYZ of pedal point P is similar to triangle ABC.
Click here to see that the pedal triangle A'B'C' is similar to the original triangle ABC. This is verified calculationally using this GSP construction; however, it is not a geometric proof. Notice that the ratios of corresponding sides are equal no matter where you move the vertices of the triangle ABC. Calculationally, triangle A'B'C' is similar to triangle ABC. Try to prove this geometrically.
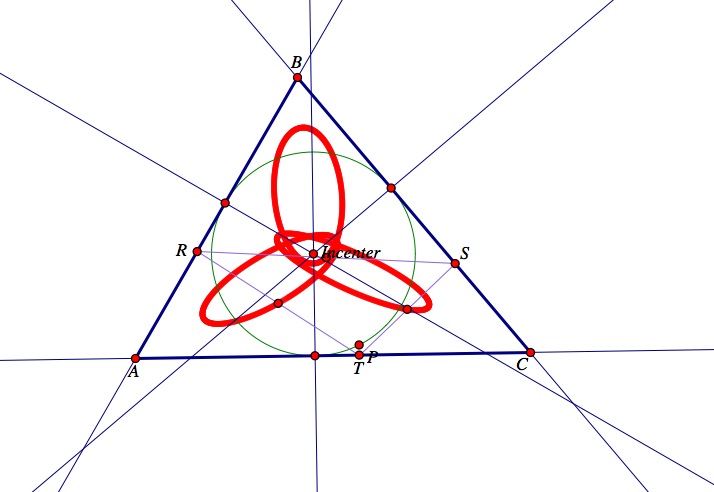
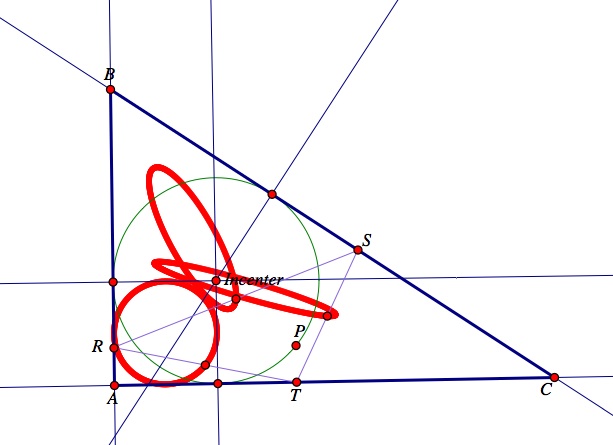
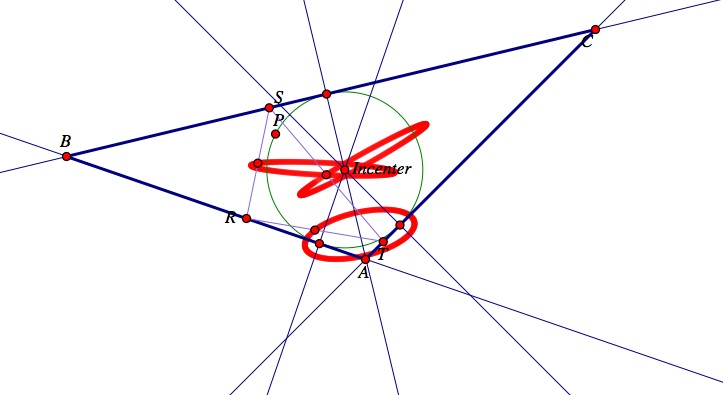
Investigation 4: Animate the Pedal point P about the incircle of ABC. Trace the loci of the midpoints of the sides. What curves result? Repeat if ABC is a right triangle.
For this investigation I began by constructing a triangle ABC and its incircle. To construct the incircle of triangle ABC, you must first construct the incenter of triangle ABC.(See instructions above on how to construct the incenter of triangle ABC). Then, construct the perpendiculars from the incenter to each side of the triangle ABC. Next, construct the intersection of the three perpendicular lines and each side of triangle ABC. Finally, construct a circle by center and point, using the incenter as the center and the intersection of one of the perpendiculars as a point. The resulting circle is the incircle of triangle ABC (shown in green). Then, I constructed the pedal triangle DEF of triangle ABC using the script tool I created in Assignment 5. Next, we want to construct the midpoints of the sides of the pedal triangle DEF, and then merge the pedal point, P, to the incircle. Below is the resulting picture.
I then traced each of the midpoints and animated the pedal point P. Click here for the GSP construction to observe the animation of the pedal point P around the incircle of triangle ABC. Below is the resulting picture when the pedal point, P, is animated and the midpoints are trace in an acute triangle.
Notice that three ellipse's are formed (shown in red) when ABC is an acute triangle. Next, observe what happens when the pedal point, P, is animated and triangle ABC is a right triangle.
Now, two ellipses and a circle are formed. Why is this?
Next, let's observe what happens when triangle ABC is an obtuse triangle.
Observe that three ellipse's are formed again when triangle ABC is obtuse.